Oszacowanie strat ciepła z obiektów można dokonać z użyciem pomiarów temperatury, w tym termowizyjnych.
Oszacowanie strat ciepła metodą pośrednią na podstawie pomiarów temperatur
Oszacowanie strat ciepła z obiektów można dokonać z użyciem pomiarów temperatury, w tym termowizyjnych. Opcję taką posiadają niektóre kamery termowizyjne w odniesieniu do powierzchni płaskich. Do takiego pomiaru wykorzystuje się prawo Fouriera, zgodnie z którym przez kolejne warstwy i jednakowe powierzchnie przenika w stanie ustalonym (to niezwykle istotny warunek) taki sam strumień ciepła q. Można go opisać równaniem (1). Prawo Fouriera wykorzystują także mierniki, w których pomiar temperatury powierzchni dokonuje się metodami stykowymi, przedstawionymi m.in. w artykule [1].

(1)
Teoretycznie do wyznaczania strumienia q użyć można każdego z członów równania, lecz z założenia nieznany jest np. opór przewodzenia wielowarstwowego izolowanego rurociągu, izolacji zbiornika czy przegrody budowlanej. Pozostaje zatem człon pierwszy związany np. z wymianą ciepła między medium a ścianką rurociągu/zbiornika czy powietrza wewnętrznego a ścianą od strony wewnętrznej lub ostatni związany z wymianą ciepła między płaszczem ochronnym izolacji lub przegrody od strony zewnętrznej a otoczeniem. Korzystając z zależności (1) i (2), można wyznaczyć również współczynnik przenikania ciepła U, wykorzystując jeden z członów równania (3)

(2)
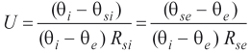
(3)
W artykule [2] padła sugestia, że można uśrednić wyniki obliczeń, licząc U zarówno z pierwszego, jak i drugiego członu równania (3), jednak z uwagą, iż praktyka badań termowizyjnych obiektów budowlanych wykazuje, że oszacowanie wartości U jest dokładniejsze od strony wewnętrznej. Wynika to przede wszystkim z faktu, że pomiar termowizyjny jest krótkotrwały, a spełnienie warunku ustalonej wymiany ciepła, przy zmiennej temperaturze zewnętrznej, jest niemal niemożliwe do spełnienia. Potwierdzają to m.in. wyniki badań przedstawione w artykule [3] dotyczącym izolacyjności przegród budowlanych. Wynika z nich, że mogąc prowadzić długotrwały pomiar temperatur, co najmniej dobę, należałoby korzystać z wartości ustalonych, co można zaobserwować, tworząc wykres zmiany w czasie współczynnika U lub na podstawie asymptot, do których zmierzają temperatury, gdy stan ustalony nie zostanie osiągnięty. Stwierdzono również, że inercja przegród budowanych powoduje, że pomiar współczynnika U z użyciem temperatur od strony wewnętrznej obarczony jest mniejszym błędem (są też mniejsze wahania temperatury zarówno przegrody, jak i powietrza).
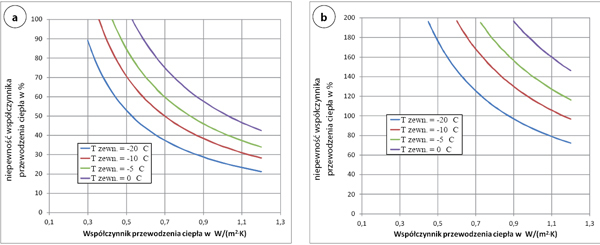
Rys. 1 Zmiana niepewności współczynnika przewodzenia U w zależności od jego wartości przy stałej różnicy temperatur wewnętrznej i zewnętrznej przy pomiarze temperatury przegrody od wewnątrz (a) i od zewnątrz (b) przy niepewności pomiarów temperatur 1oC
Ze względu na złożoną postać wyrażenia określającego współczynnik U przeprowadzono oszacowania niepewności U metodą Monte Carlo, generując 106 wyników i na ich podstawie wyznaczono niepewność wyznaczenia U. Założono w tym momencie, że niepewność pomiaru temperatur jest na poziomie 1oC, a współczynniki Rsi lub Rse są bezbłędne. Uzyskane wyniki pokazano na wykresach na rys. 1. Niepewność wyznaczania współczynnika U na poziomie nie mniejszym niż 20% występuje dla różnicy temperatur wewnętrznej i zewnętrznej równej 40oC i to dla dużej wartości współczynnika U > 1,2 W/(m2K), gdy dokonuje się pomiaru temperatury od wewnątrz przegrody budowlanej. W miarę jak maleje współczynnik U, niepewność wyznaczania U rośnie do niemal 100% dla U < 0,3 W/(m2K). Jeszcze gorsza sytuacja występuje, gdy podstawą wyznaczania U będzie pomiar temperatury przegrody od zewnątrz. Tu w analogicznych warunkach w najlepszym przypadku niepewność wyznaczenia U osiągnie 80%. Nie należy zatem się dziwić, gdy współczynnik U ustalony dla obu wariantów różni się kilkakrotnie. Ich uśrednianie będzie błędem. Oczywiście nie wyklucza to sytuacji, że uzyskać można zbieżne wyniki. Jest to jednak rzadka sytuacja, jeżeli nie zmniejszy się niepewności pomiaru temperatury.
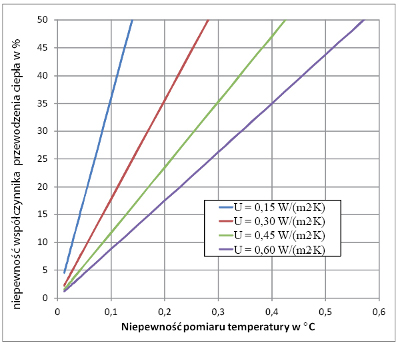
Rys. 2 Zmiana niepewności współczynnika przewodzenia U w zależności od niepewności pomiaru temperatur przy pomiarze temperatury przegrody od wewnątrz
Dokonano również obliczeń wpływu niepewności pomiaru temperatury (dla uproszczenia przyjęto jednakową wartość dla wszystkich pomiarów) na niepewność U dla kilku wartości U. Wyniki w postaci charakterystyk dla różnicy temperatur 40oC pokazano na rys. 2. Realne jest uzyskanie niepewności pomiaru temperatury przy pomiarze punktowym (metodą kontaktową) na poziomie 0,1oC, jednak i tak w tym przypadku niepewność wyznaczania współczynnika U, przegrody o współczynniku U = 0,15 W/(m2K), wynosi aż 35%. Natomiast współczynnik U = 0,75 W/(m2K) zostanie wyznaczony z niepewnością 7%. Praktycznie tylko w pomiarach laboratoryjnych taką metodą można wyznaczyć z kilkuprocentową niepewnością współczynnik U, gdy niepewność pomiaru temperatury wynosi 0,01oC.
Wykonując analogiczne obliczenia niepewności jednostkowych strat ciepła, uzyskuje się niemal takie same wartości niepewności oszacowania strumienia strat ciepła q.
Reasumując, dokładny pomiar temperatury zarówno mediów otaczających przegrody izolacyjne, jak i temperatur powierzchni tych przegród jest podstawą uzyskania wiarygodnego oszacowania. Niepewność pomiaru temperatury liniowo przekłada się na niepewność pomiaru zarówno strumienia traconego ciepła, jak i współczynników przewodzenia ciepła. Im lepsze są właściwości izolacyjne przegród lub osłon, tym trudniej uzyskać jest wiarygodny wynik oszacowania ww. parametrów.
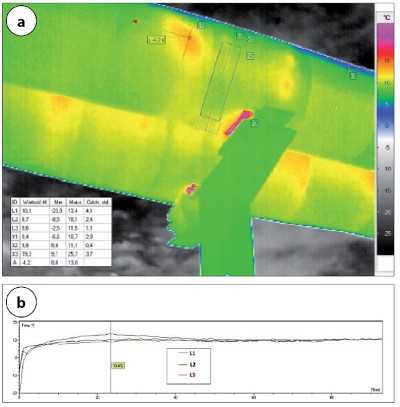
Rys. 3 Termogram (a) i histogramy (b) temperatury rurociągu o wysokim współczynniku emisyjności płaszcza podczas pochmurnego dnia
Pomiar strat ciepła z użyciem kamery termowizyjnej
Jak to już zostało przedstawione, wymiana ciepła zarówno od strony wewnętrznej, jak i zewnętrznej zależy od wielu czynników. Uzyskanie wiarygodnych oszacowań strat ciepła na podstawie pomiarów temperatury jest trudne i wymaga nie tylko dokładnych pomiarów temperatury, lecz również pomiaru prędkości powietrza w przypadku instalacji zewnętrznych.
Na końcową niepewność pomiaru strumienia ciepła wpływają niepewności pomiaru parametrów, wśród których kluczowa jest niepewność pomiaru temperatur, a ta w przypadku kamer termowizyjnych nie jest mała. Większość kamer termowizyjnych oferuje niepewność pomiaru temperatury nie mniejszą niż 2oC, pod warunkiem że prawidłowo zostaną ustalone i wprowadzone pozostałe parametry, minimalnie, takie jak współczynnik emisyjności ei temperatura otoczenia qe. Gdy pomiar jest wykonywany z większej odległości, konieczne jest wprowadzenie temperatury otaczającego powietrza oraz współczynnika transmitancji bądź tłumienia atmosfery.
Praktyczna metoda pozwalająca poprawnie określić emisyjność obiektu wymaga stykowego dokładnego pomiaru temperatury obiektu. Na termogramie należy zmniejszać wartość współczynnika emisyjności do momentu aż temperatura na termogramie, w obszarze pomiaru stykowego, będzie dokładnie taka sama jak z metody stykowej. Znane są też inne metody, polegające na wykorzystaniu lub stworzeniu obszaru zachowującego się jak ciało czarne. Można wykorzystać odpowiednio głębokie otwory lub jeśli jest to dopuszczalne, pokryć obiekt miejscowo czarną matową farbą. Można wtedy uznać, że w tych miejscach e»1, a korektę współczynnika emisyjności mierzonego obszaru należy prowadzić aż do otrzymania takich samych temperatur. Można uznać, że po takiej „kalibracji” niepewność pomiaru temperatury z termogramu jest zbliżona do niepewności pomiaru metodą stykową, jednak tylko dla wybranego materiału, dla którego określono w ten sposób doświadczalnie e.
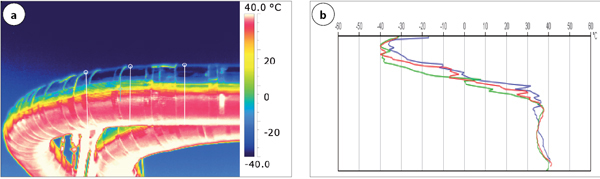
Rys. 4 Termogram (a) i histogram (b) temperatury rurociągu o niskim współczynniku emisyjności płaszcza podczas słonecznego dnia
Drugi parametr, który musi być poprawnie wprowadzony do kamery, to temperatura otoczenia. Jak już wspomniano, nie jest to temperatura otaczającego powietrza, a jej określenie jest trudne, w niektórych przypadkach wręcz niemożliwe, gdy jednocześnie nie dokonano uzupełniających pomiarów. Problemy związane z radiacyjną wymianą ciepła rurociągów napowietrznych przedstawiono m.in. w [4], natomiast możliwość wykorzystania kamery termowizyjnej do pomiaru promieniowania cieplnego nieboskłonu, w celu poprawnego wyznaczenia temperatury otoczenia do obliczeń wymiany ciepła, przedstawiono w [5]. Optymalne warunki pomiaru w przestrzeni zewnętrznej to równomierne zachmurzenie, kiedy temperatura nieboskłonu jest stosunkowo wysoka (dodatnia) i możemy ją określić na podstawie pomiaru kamerą termowizyjną, kierując ją w to miejsce, które się odbija w mierzonym obiekcie. Przykład termogramu wykonanego w pochmurny dzień i profilów temperatury pokazano na rys. 3.
Dla kontrastu na rys. 4 pokazano wykonany w bezchmurny dzień termogram i profile temperatury płaszcza rurociągu. Widać bardzo dużą asymetrię temperatur górnej i dolnej części płaszcza spowodowaną odbiciem nieboskłonu. Bezchmurne niebo ma temperaturę radiacyjną często poniżej dolnego zakresu pomiarowego większości kamer termowizyjnych.
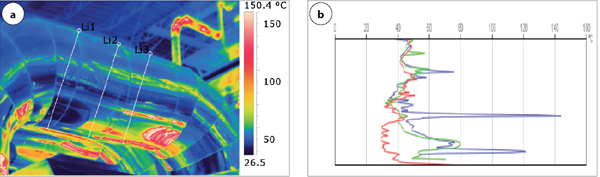
Rys. 5 Efekt odbicia termicznego elementów armatury o wysokiej temperaturze w osłonie izolacji rurociągów parowych
Problemy z odbiciami występują także w przestrzeniach zamkniętych, co przedstawiono na rys. 5 i 6.
Termogramy i histogramy zarówno dla obiektów o stosunkowo niskim współczynniku emisyjności (e= 0,5; rys. 5), jak i dla wyższego współczynnika emisyjności (e= 0,7; rys. 6) dowodzą, że nieuwzględnienie odbicia prowadzić będzie do zawyżenia lub zaniżenia wyników pomiarów temperatury.
Nieuwzględnienie faktu odbicia termicznego otoczenia podczas pomiarów prowadzi do dużo większych błędów niż podstawowa niepewność pomiaru temperatury kamerami, a wyznaczenie strat ciepła skończy się fiaskiem.
Oprócz omawianych kwestii termicznego odbicia obiektów istotny jest jeszcze jeden problem związany z pomiarem termowizyjnym. Dla kątów obserwacji większych od 50–60o ciała rzeczywiste nie spełniają w sposób ścisły prawa Lamberta odnoszącego się do ciał doskonale czarnych. Zgodnie ze wspomnianym prawem natężenie promieniowania powierzchni widzianej pod kątem jest niezależne od tego kąta. Nawet dla materiałów o współczynniku emisyjności zbliżonym do jedności zbyt duży kąt obserwacji powoduje pozorne zmniejszenie współczynnika emisyjności (rys. 7a), co wywołuje zaniżenie wyniku pomiaru temperatury. Skutek tego jest widoczny zarówno na termogramie, jak i profilu temperatury rurociągu zaprezentowanego na rys. 7b.
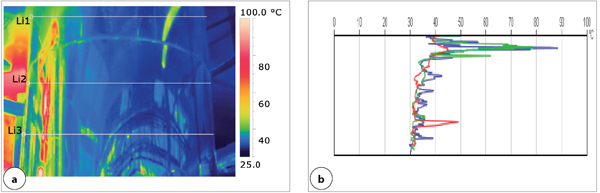
Rys. 6 Odbicie na termogramie elementów wysokotemperaturowych armatury oraz niskotemperaturowych konstrukcji hali w osłonie termicznej
Podsumowując, podczas pomiaru termowizyjnego wskazane jest skierować kamerę nie tylko na obiekt pomiarowy, ale i na to, co się może w nim odbić. Pozwoli to na stwierdzenie i skompensowanie problemu związanego z odbiciami. Można też zastosować strategię „omijania” miejsc, w których następują odbicia, ale nie zawsze można jej użyć. Jeśli to możliwe, powinno się wykonać kilka pomiarów z różnych punktów obserwacji, przy zachowaniu zasady związanej z kątem obserwacji (nie większym od 50o), zwracając przy tym uwagę na możliwość odbicia na termogramie samego operatora. Nieuwzględnienie dodatkowych czynników związanych z otoczeniem prowadzić może do dużo większych błędów pomiaru temperatury niż podstawowa wartość niepewności pomiaru kamery. Wykorzystanie takich termogramów dyskwalifikuje je do użycia w celu oszacowania strat ciepła.

Rys. 7 Pozorna zmiana współczynnika emisyjności (a) i temperatury rurociągu (b) spowodowane zmianą kąta pomiaru
Wnioski
Pomiar rzeczywistych strat ciepła z instalacji jest zadaniem trudnym, nawet wtedy gdy dysponuje się specjalistycznym sprzętem pomiarowym. Najlepsze efekty uzyskać można przez bezpośredni pomiar. Metody obliczeniowe można wykorzystać zarówno do obliczeń, wtedy gdy znane są właściwości fizyczne materiałów i geometria obiektu, jak i w pomiarach pośrednich. O ile w obliczeniach przyjmuje się warunki odniesienia opisujące konwekcyjną i radiacyjną wymianę ciepła, o tyle w pomiarach warunki te należy zmierzyć i uwzględnić, przeliczając wyniki do obliczeniowych warunków odniesienia.
Jednym z narzędzi, które można użyć do pomiarów strat ciepła, może być kamera termowizyjna, jednak uzyskanie niepewności wyniku na poziomie 20–30% może być trudne, bez dodatkowych zabiegów. Należy liczyć się z sytuacją, że oszacowanie strat ciepła różnymi metodami prowadzić będzie do znacznie różniących się wyników, co starano się wyjaśnić w niniejszej publikacji.
dr hab. inż. Sławomir Zator
Wydział Inżynierii Produkcji i Logistyki Politechniki Opolskiej
Marta Zator
studentka Wydziału Architektury Politechniki Wrocławskiej
Literatura
1. O. Niemyjski, Straty ciepła w sieciach ciepłowniczych, „Inżynier Budownictwa” nr 9/2013, dodatek specjalny Ciepłownictwo i ogrzewnictwo.
2. B. Więcek, R. Strykowski, Ilościowe aspekty zastosowania termowizji w budownictwie, „Inżynier Budownictwa” nr 2/2013.
3. A. Wróbel, A. Wróbel, Kontrola termograficzna izolacyjności cieplnej nowo wzniesionych budynków mieszkalnych, cz. II, „Inżynier Budownictwa” nr 4/2011.
4. T. Kruczek, A. Fic, Wpływ radiacyjnej wymiany ciepła na rozkład temperatury na powierzchni płaszcza napowietrznego rurociągu ciepłowniczego w warunkach niskiej temperatury nieboskłonu, „Modelowanie Inżynierskie” nr 6/2012, t. 12, z. 43.
5. T. Kruczek, Zastosowanie kamery termowizyjnej LW w pomiarze cieplnego promieniowania nieboskłonu, „Pomiary Automatyka Kontrola” nr 9/2013.